The End of Space-time
Physics-Mathematics
DOI:
https://doi.org/10.14331/ijfps.2020.330139Keywords:
space-time, time-invariant space, entropy, bijective research methodologyAbstract
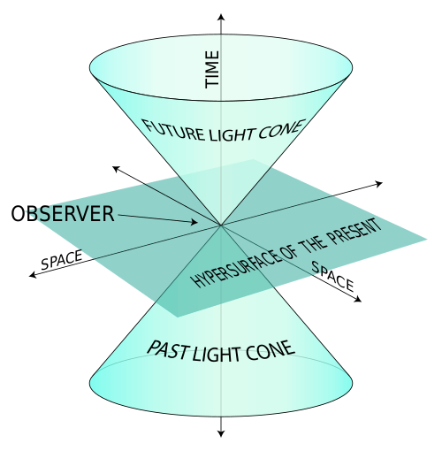
In bijective modeling, the physical reality is represented by the set X, the model of physical reality by the set Y. Every element in the set X has exactly one correspondent element in the set Y. Set X and set Y are related by the bijective function f : X -> Y. Bijective modeling is confirming that time is the duration of given system entropy increasing in time-invariant space.
Downloads
Author Biographies
Amrit Šorli, Bijective Physics Institute
Amrit S. Šorli is the founder and the director of a private research organization “Bijective Physics Institute – BPI”. He developed a bijective research methodology based on the bijective function of set theory. His main research subjects are the foundations of physics, time, gravity, superfluid quantum space, the Theory of Relativity, and cosmology. He published around 60 research articles and 10 books.
Štefan Čelan, Scientific Researcg Centre Bistra, Ptuj, Slovenia
Štefan Čelan is the founder and the director of Scientific Research Centre Bistra. In 2019, ZRS Bistra Ptuj received the title of Regiostars Winner for the most innovative project in the competition of 28 countries in the EU. He holds a Ph.D. in chemical technology and also has an interest in the foundations of physic, gravity, and cosmology. In addition to expert articles published in foreign and domestic scientific journals, the co-author and co-owner of several patents. With two patents, he appeared at international patent and innovation fairs in Geneva and Nuremberg and received silver medals. He has been named Industry Innovator of the Year several times.
References
Ben-Naim, Arieh. (2020). Entropy and Time. Entropy, 22(4), 430.
Buhusi, Catalin V, & Meck, Warren H. (2005). What makes us tick? Functional and neural mechanisms of interval timing. Nature reviews neuroscience, 6(10), 755-765.
Ebadi, Behrooz. (2019). Arrow of time: A physical concept with philosophical roots: Philosophy of physics. International Journal of Fundamental Physical Science, 9(3), 37-40.
Fiscaletti, Davide, & Sorli, Amrit. (2015). Perspectives of the numerical order of material changes in timeless approaches in physics. Foundations of Physics, 45(2), 105-133.
Fiscaletti, Davide, & Sorli, Amrit. (2017). Searching for an adequate relation between time and entanglement. Quantum Studies: Mathematics and Foundations, 4(4), 357-374.
Fursaev, Dmitri V. (2006). Entanglement entropy in critical phenomena and analog models of quantum gravity. Physical Review D, 73(12), 124025.
Hawking, Stephen W. (1985). Arrow of time in cosmology. Physical Review D, 32(10), 2489.
Horwitz, Lawrence P. (2019). Stueckelberg-Horwitz-Piron Canonical Quantum Theory in General Relativity and Bekenstein-Sanders Gauge Fields for TeVeS Progress in Relativity: IntechOpen.
Horwitz, LP. (2020). The Relativistic Boltzmann Equation and Two Times. Entropy, 22(8), 804.
Ivry, Richard B, & Spencer, Rebecca MC. (2004). The neural representation of time. Current opinion in neurobiology, 14(2), 225-232.
Lehto, M, Nielsen, Holger B, & Ninomiya, Masao. (1989). Time translational symmetry. Physics Letters B, 219(1), 87-91.
Lucia, Umberto, Grisolia, Giulia, & Kuzemsky, Alexander L. (2020). Time, Irreversibility and Entropy Production in Nonequilibrium Systems. Entropy, 22(8), 887.
Mauk, Michael D, & Buonomano, Dean V. (2004). The neural basis of temporal processing. Annu. Rev. Neurosci., 27, 307-340.
Müller, Clemens, Guan, Shengwei, Vogt, Nicolas, Cole, Jared H, & Stace, Thomas M. (2018). Passive on-chip superconducting circulator using a ring of tunnel junctions. Physical review letters, 120(21), 213602.
Šorli, Amrit Srečko. (2019). Mass–Energy Equivalence Extension onto a Superfluid Quantum Vacuum. Scientific reports, 9(1), 1-9.
Strauss, Yossef, Silman, Jonathan, Machnes, Shai, & Horwitz, Lawrence P. (2011). Study of a self-adjoint operator indicating the direction of time within standard quantum mechanics. arXiv preprint arXiv:1101.3969.
t Hooft, Gerard. (2018). Time, the arrow of time, and Quantum Mechanics. Frontiers in Physics, 6, 81.
Wittgenstein, Ludwig, & dos Santos, Luiz Henrique Lopes. (1994). Tractatus logico-philosophicus: Edusp.
Published
How to Cite
Issue
Section
License
Copyright (c) 2020 International Journal of Fundamental Physical Science
This work is licensed under a Creative Commons Attribution 4.0 International License.
